Л5 – Семантичні мережі

ЛЕКЦІЯ-5.

3.4. Семантичні мережі

3.4.1. Загальне поняття про семантичні мережі

Семантичні мережі не є однорідним класом моделей представлення знань. Часто загальною основою віднесення схеми представлення знань до семантичної мережі є те, що вона представляється у вигляді спрямованого графа, вершини якого відповідають об’єктам (поняттям, сутностям) предметної області, а дуги – відносинам (зв’язкам) між ними. І вузли, і дуги, як правило, мають мітки (імена), Імена вершин і дуг звичайно збігаються з іменами відповідних об’єктів і відносин предметної області.

Об’єкти предметної області, що відображаються в семантичній мережі, можна умовно розділити на три групи: узагальнені, індивідуальні (конкретні) і агрегатні об’єкти.

Загалиний об’єкт відповідає деякій збірній абстракції реально існуючого об’єкта, чи процесу явища предметної області. Наприклад, “виріб”, “підприємство”, “співробітник” і т.д. Узагальнені об’єкти фактично представляють визначені класи предметної області.

Індивідуальний об’єкт – це певним чином вигляділений одиничний представник (екземпляр) класу. Наприклад, “співробітник Петров И.Н.” Агрегатним називається складений об’єкт, утворений з інших об’єктів, що розглядаються як його складові частини. Наприклад, виріб складається з сукупності деталей, підприємство складається з сукупності відділів, служб, цехів.

Введена класифікація об’єктів є відносно. В залежності від розв’язуваної задачі той самий об’єкт може розглядатися як узагальнений чи індивідний, як агрегатний чи неагрегатний.

Типи, зв’язків між об’єктами семантичних мереж можуть бути будь-якими. Але найчастіше застосовуються наступні основні зв’язки (відносини): “рід-вид”, “є представником”, “є частиною”. Наявність зв’язку типу “рід-вид” між узагальненими об’єктами А і В означає, що поняття А більш загальне, ніж поняття В. Будь-який об’єкт, що відображається поняттям В, відображається і поняттям А, але не навпаки. Наприклад, поняття “тварина” – це родове поняття для о’бъекта “птах”. Усі властивості родового об’єкта А, як правило, притаманні і видовому об’єкту В. Іншими словами, об’єкт В успадковує властивості об’єкта А.

Зв’язок “є представником” існує звичайно між узагальненим та індивідним об’єктом, коли індивідний об’єкт виступає в ролі представника деякого класу. Так, індивідний об’єкт “вівчарка Альма” є представником (екземпляром) узагальненого об’єкта “вівчарка”. Екземпляр може бути представником декількох узагальнених об’єктів. У цьому випадку йому притаманні властивості декількох узагальнених об’єктів, що відповідають множинному успадкуванню.

У ряді випадків між зв’язками “рід-вид” і “є представником” не роблять розбіжностей, відзначаючи, що ці зв’язки задають відношення “загальна-частка” (Рисунок 3.7). Іноді це приводить до непорозумінь. Тому для формалізації таких зв’язків будемо використовувати відносини аkо (від англ. a-kind-of – різновид) і іs а (від англ. іs a member of the class -бути представником класу) [94].

Не менш важливе відношення “є частиною” (англ. part of). Дане відношення зв’язує агрегатний об’єкт із його складовими частинами. Воно дозволяє відбивати в базі знань структуру об’єктів предметної області. Іноді дане відношення позначають міткою “має” (англ. has).

Як приклад нa рисунку зображена семантична мережа, що представляє частину знань про тваринний світ.

Дана мережа була розроблена A.M. Коллінзом і М.Р. Куілліаном (1969) і використовувалася, для моделювання механізмів пам’яті людини. Завдяки відносинам аkо мережа являє собою якусь ієрархічну структуру і дозволяє відповідати на такі питання, як: “чи є канарка птахом?”, “чи може канарка літати?” і т.д. У ході експериментів із представленою моделлю було встановлено, що людина прагне запам’ятовувати інформацію, що відповідає найбільш абстрактному рівню. Наприклад, замість того, щоб безпосередньо запам’ятовувати факт “канарка вміє літати”, людина представляє цей факт у вигляді властивості, і зв’язує його з поняттям “птах”. Аналогічно властивості: “дихати”, “їсти”, “переміщатися” – зв’язуються з поняттям “тварина”. Такий метод запам’ятовування інформації дозволяє виключити її дублювання в базі знань завдяки спадкуванню властивостей у відповідності з аkо ієрархією. Наприклад, властивість “мати крила” притаманне птахам, отже, воно притаманне і канарці.

Рисунок 3.7 – Світ тварин у вигляді семантичної мережі.

Вперше семантичні мережі з’явилися в області машинної лінгвистики як засіб аналізу змісту (семантики) природної мови. У 1967 році М.Р. Куілліаном була розроблена програма, що фіксує зміст англійських слів, побудована за принципом тлумачного словника. У цій програмі деяке слово англійської мови визначається в термінах, що виражаються іншими словами. Кожне слово визначається множиною покажчиків на інші слова. Сукупність вказівників утворить мережу, “подорожуючи” у якій можна з’ясувати зміст того чи іншого слова. У семантичній мережі Куілліана вершини відповідають обумовленому поняттю і забезпечуються вказівниками на інші слова, що розкривають дане поняття. База знань організована у вигляді сторінок (площин), на кожній з який представляється граф, що визначає одне слово. На рисунку 3.8 зображені три різних визначення англійського слова “plant”. Вказівники, позначені на рисунку 3.8 суцільними стрільцями, формують наступні визначення слова “plant “;

1)    жива (lіve) структура (structure), що не відноситься до тварин (anіmal), часто має листи (leaf), одержує (get) харчування (food) з (from) повітря (aіr), води (water) і ґрунту (earth);

2)    устаткування (апаратура – apparatus), використовуване (use) для (for) реалізацій будь-якого процесу (process) у (іn) промисловості (іndustry);

3)    поміщати (put) щось (seed – насіння, plant – рослина і т.п.) у ґрунт (earth) для (for) вирощування (grow)

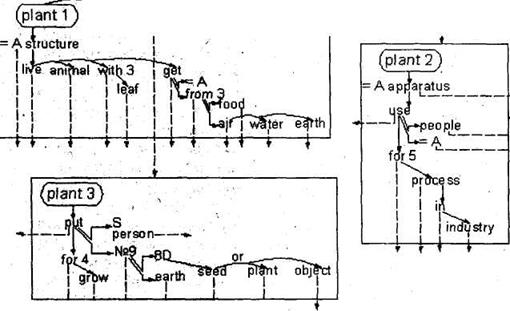
Рисунок 3.8-визначення слова “plant”

Перше визначення (plant 1) відповідає іменнику “рослина”, друге (plant 2) – іменнику “завод”, третє (plant 3) – дієслову “садити”. Вказівники, позначені на рисунку штриховими лініями, посилаються на слова-поняття, представлені на інших сторінках.

Один з механізмів виводу, що застосовується у розглянутій моделі семантичної мережі, заснований на пошуку по перетинанню. Він дозволяє встановлювати стосунки між двома словами. Пошук виконується методом у ширину по зовнішніх вказівниках із двох вихідних сторінок доти, поки не буде знайдено загальне поняття, що відповідає вершині перетинання двох напрямків пошуку. Знайдені в результаті пошуку шляху від вихідних вершин до вершини перетинання і будуть представляти відношення між вихідними словами-поняттями. Наприклад, слова-поняття “cry” (плач, плакати) і “comfort” (розрада, утішати) приводять до перетинання шляхів пошуку у вершині “sad” (сумний, сумовитий). У результаті аналізу шляхів пошуку модель дозволяє зробити наступний вивід:

“Плач – це один зі способів створення сумних звуків. Утішати – робити щось менш сумним”.

Таким чином, модель дозволяє формувати відносини, що представлені в ній неявно отже, на її основі можна одержувати нові знання. Це дозволяє будувати системи розуміння прирідної мови, що володіють наступними можливостями [77]:

1)    визначати основний зміст тексту шляхом пошуку множини вершин перетинання;

2)    здійснювати вибір необхідного значення багатозначного слова на основі найкоротшого шляху від цього слова до інших слів розглянутої пропозиції (свого роду семантична метрика);

3)    формувати відповіді на різні запити шляхом встановлення взаємозв’язків між словами-поняттями запиту і словами-поняттями, що зберігаються в пам’яті системи.

Розглянутий підхід одержав деякий розвиток у системі TLC (Teachable Language Comprehender: навчальна система розуміння мови), що розроблена Квілліаном. Однак практичний успіх TLC був обмежений. Це мається на увазі тому, що набір використовуваних типів зв’язків (відносин) між поняттями був недостатній. Використовувалися тільки такі зв’язки, як: “класс – екземпляр класу”, “атрибут.- значення”. Окрім цього, сам пошук не враховував зміст зв’язків. Представлення знань вимагає введення в розгляд більш багатого набору відносин між поняттями (об’єктами, сутностями) предметної області. Подальший розвиток мережних моделей представлення знань здійснювався саме в цьому напрямку. Роботи Р.Симмонса і К.Филмора вказали на важливу роль дієслів при аналізі змісту пропозицій природної мови. Пропозицію можна представити вершиною-дієсловом і різними відмінковими зв’язками (відносинами). Таку структуру називають відмінковою рамкою. Серед відмінкових відносин вигляділяють наступні: агент – відношення між подією і тим хто (що) його робить; об’єкт – відношення між подією і тим, над чим виконується дія; інструмент – об’єкт, за допомогою якого відбувається дія; місце – місце здійснення події; час – час здійснення події. При аналізі пропозиції програма знаходить дієслово і встановлює відповідні відмінкові відносини між частинами пропозиції. Як приклад на рисунку 3.9 зображена відмінкова рамка пропозиції: “Іван закріпв деталь клеєм”. Відмінкова рамка фіксує знання відмінкової (лінгвістичної) структури природних мов у вигляді мережного формалізму.

У відповідності з введеним раніше визначенням семантичної мережі, відсутні будь-які обмеження як на типи відносин, так і на типи об’єктів, відображуваних у мережі. У більшості випадків різноманіття об’єктів мережі можна розділити на три групи [29,16]:

1. об’єкта-поняття- зведення про фізичні й абстрактні об’єкти, предметну область;
   
2. об’єкта-події- абстрактні чи конкретні дії, що можуть привести до зміни стану предметної області;
   
3. об’єкта-властивості – уточнюють поняття і події, наприклад, указують характеристики понять (колір, форму, розміри і т.п.), фіксують параметри подій (місце, час, тривалість).
   

Рисунок 3:9 – Відмінкова рамка

Різноманіття відносин, що використовуються у семантичних мережах, підрозділяються на наступні групи:

1. лінгвістичні відносини, що, у свою чергу, підрозділяються на відмінкові (агент, об’єкт, інструмент, час, місце), дієслівні (нахилення, час, вид, число, застава) і атрибутивні (колір, розмір, форма і т.п.);
   
2. логічні відносини (кон’юнкция, диз’юнкція, заперечення, імплікація);
   
3. теоретико-множинні відносини містять у собі відносини типу “множину-підмножина” (”рід-вид”, “клас-підклас”), “ціле-частина”, “елемент множини” і ін.
   
4. квантифіковані відносини, що підрозділяються на логічні квантори спільності й існування, нечіткі квантори (багато, трохи, часто т.д.).
   

   Таким чином, розглянуті раніше відносини, (“рід-вид”, “бути представником”, “бути частиною”, відмінкові відносини) далеко не вичерпують усього набору відносин, застосовуваних у семантичних мережах. Але вони утворять гарну основу для побудови прикладних баз знань. Особливе місце при цьому займають теоретико-множинні відносини, що володіють транзитивними властивостями. Відношення R називається транзитивним, якщо для будь-яких об’єктів таких, що знаходиться у відношенні – у відношенні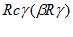, випливає справедливість твердження “ знаходиться у відношенні R c “
   , тобто
   

   
   

   Наприклад, транзитивність родовидових відносин забезпечує можливість спадкування властивостей від родового об’єкта до виду і підвиду. Механізм спадкування властивостей забезпечує проведення найпростіших дедуктивних висновків типу: “Усі люди смертні. Сократ – людина. Отже, Сократ смертний” [34].
   

   У базах знань вигляділяють інтенсіональні і єкстенсіональні знання. Якщо є кінцева множину атрибутів А={А₁, А₂, …, А_n} і кінцева множинf відносин R={ R₁, R₂, …, R_m }, то схемою чи інтенсіоналом відносини R_i{і=l,2,…,m) називається набір пар виду.
   

   ІNT(R_i )={…,[ A_j , DOM(A_j)],…},
   

   де DOM(A_j) – домен атрибута A_j, тобто множину можливих значень атрибута. Екстенсіонал відносини R_i,- – це множина фактів,
   

   EXT(R_i)={ F₁, F₂, …, F_p }
   

   де F₁, F₂, …, F_p – факти відносини R_i, що задаються звичайно у вигляді сукупності пар “атрибут-значення”. Факт конкретизує визначене відношення. У графічній інтерпретації він являє собою подграф, що має зіркоподібну структуру. Коренем подграфа є вершина предикатного типу з міткою, що відповідає імені відносин. Ребра підграфа відзначені іменами атрибутів.
   

   Інтенсіональна семантична мережа представляє предметну область, що моделюється на узагальненому, концептуальному рівні, а єкстенсіональна – наповнює її конкретними, фактичними даними. Таким чином, семантичну базу знань можна розглядати як сукупність об’єктів і відносин, частина з яких визначена інтенсионально, а частина – єкстенсионально.
   

   3.4.2. Способи опису семантичних мереж і логічний вивід
   

   Після знайомства з загальними поняттями семантичних мереж розглянемо способи опису семантичних мереж. Найчастіше для цих цілей використовують концептуальні графи Дж. Соува і блокові структури Г.Хендрікса. Блокові структури докладно описані в [8,35]. Тому розглянемо опис семантичних мереж у вигляді концептуальних графів.
   

   Вершинами концептуального графа є або об’єкти (поняття, сутності) предметної області, або концептуальні відносини. Ребра концептуального графа зв’язують між собою поняття-вершини-поняття і відносини-вершина-відносини. При цьому ребра можуть виходити з вершини-поняття і закінчуватися в ставленні-вершині-відношенні, і навпаки. На рисунку 3.10 вершини “м’яч” і “червоний” відповідають вершинам-поняттям, а вершина “колір” – бінарному відношенню. Для того щоб розрізняти зазначені типи вершин, на концептуальних графах їх зображують прямокутником і еліпсом, відповідно.
   

   Одне з переваг вигляділення відносин у самостійні вершини концептуального графа полягає в спрощенні представлення парных відносин. Таке відношення представляється ставленням-вершиною-відношенням з n-ребрами (Рисунок 3.10).
   

   
   

   Рисунок 3.10 – Приклади концептуальних графів
   

   Зазвичай кожний концептуальний граф фіксує одне речення. Тоді база знань будет представлятись у вигляді сукупності таких графов. Наприклад, верхній граф на рисунку 3.10 відповідає реченню “Мяч має червоний колір”. Граф, що зображений на рисунку 3.11, відображає більш складне речення: “Іван закріпив деталь стільця клеєм”.
   

   
   

   Рисунок 3.11 – Концептуальний граф пропозиції
   

   Цей граф використовує відмінкові відносини дієслова “закріпити” і демонструє можливості концептуальних графів для представлення пропозицій прирідної мови.
   

   Кожна поняття-вершина-поняття концептуального графа може мати мітку типу. Тип позначає клас приналежності вершини. На концептуальному графі мітку типу вершини відокремлюють двокрапкою від конкретного імені вершини. На рисунку 3.11 за допомогою мітки типу показано, що Іван є столяром. На концептуальних графах можна також вводити індивідні поняття-вершини-поняття з однаковими іменами. Щоб розрізняти єкземпляри об’єктів (понять) з однаковими іменами, використовується спеціальний числовий маркер, перед яким записаний символ #. Граф на рисунку 3.12 вказує, що конкретний “автомобіль” з маркером #1235 має зелений колір.
   

   
   

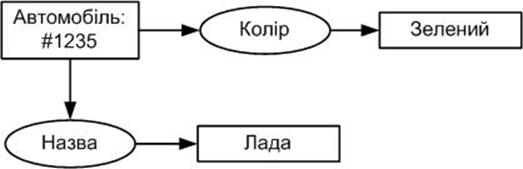
   Рисунок 3.12- Концептуальний граф з числовим маркером
   

   Крім числового маркера, на концептуальних графах можуть застосовуватися узагальнені маркери, що позначаються знаком *. У сполученні з змінною, що записується після цього знака, узагальнений маркер виявляється корисним у ситуаціях, коли дві різні вершини графа представляють той самий об’єкт. На відміну від числових маркерів, що застосовуються для вигляділення в семантичній мережі індивідних об’єктів, узагальнені маркери дозволяють вигляділяти той самий узагальнений об’єкт заданого типу (Рисунок 3.13). Як приклад на рисунку зображений концептуальний граф, що відповідає пропозиції: “Маляр забруднив свою руку фарбою”.
   

   
   

   Рисунок 3.13 – Концептуарний граф з загальним маркером
   

   На концептуальних графах вводяться операції, що дозволяють виконувати їхнє перетворення. Нові графи виходять за допомогою чотирьох операцій: копіювання, спеціалізації, об’єднання і спрощення. Розглянемо їх докладніше.
   

   Операція копіювання дозволяє сформувати з вихідного графа G його копію, наприклад, G₁.
   

   Операція спеціалізації полягає в заміні узагальненої вершини її індивідним (конкретним) варіантом. При цьому може бути два випадки:
   

   1)    якщо вершина відзначена узагальненим маркером, те узагальнений маркер заміняють конкретним індивідним маркером (іменним чи числовим).
   

   2)    тип вершини можна замінити відповідними підтипами, що володіє необхідними властивостями.
   

   Операція об’єднання дозволяє одержувати з двох графів один. Якщо на графі G₁ мається вершина-поняття V₁, що аналогічна вершині-поняттю V₂ графа G₂, то можна сформувати новий граф G₃ видаливши V₂. При цьому всі зв’язки V₂ необхідно переорієнтувати з V₂ на V₁.
   

   Операція спрощення дозволяє виключити на графах дублікати відносин. При цьому виключаються ставлення-вершина-відношення і зв’язані з нею дуги. Дублювання відносин часто виникає в результаті виконання операції об’єднання.
   

   Операція спеціалізації дозволяє зіставляти двох вершин концептуального графа і, якщо зпівставлення успішне, виконувати об’єднання. Спільне використання операцій спеціалізації й об’єднання забезпечує реалізацію механізму спадкування. Наприклад, замінивши узагальнений маркер індивідним, ми поширюємо властивості типу на конкретний індивідний об’єкт. Якщо, у ході виконання операції обмеження, відбувається заміна типу на його підтип, то має місце спадкування “підклас-клас-підклас”.
   

   Операції спеціалізації й об’єднання конкретизують вихідний граф. Якщо граф G₁ – це конкретизація графа G₂, то можна сказати, що істинно і зворотно, тобто G₂ – є узагальнення G₁. Узагальнення широке використовується при навчанні СШІ, дозволяючи виводити правдоподібні умови по приватних прикладах (див. §4.3).
   

   Розглянуті вище найпростіші операції не гарантують одержання правильних тверджень на основі перетворених графів. Конкретизація вершин-понять, виконувана в ході операцій спеціалізації й об’єднання, не завжди відповідає дійсності. Наприклад, якщо в ході виконання операції об’єднання з’єднуються два графи, агенти яких позначені тим самим поняттям, то це зовсім не означає, що не може статись так, що ці поняття відповідають двом різним індивідним об’єктам. Наприклад, пропозиціїї “Собака гризе кістку” і “Собака знаходиться в парку” можна об’єднати в одне, якщо мова йде про одне й ту саму тварину, а не про двох різних тварин. Проте, розглянуті операції не приводять до тверджень, позбавлених змісту, і дозволяють виконувати правдоподібні міркування.
   

   Концептуальні графи можуть містити вершини, що є пропозиціями. Такі вершини зображуються у вигляді прямокутного блоку, що містить підграф, що відповідає пропозиції. Як приклад на рисунку 3.14 зображений граф твердження: “Олексій думає, що Тетяні подобається іграшка”.
   

   
   

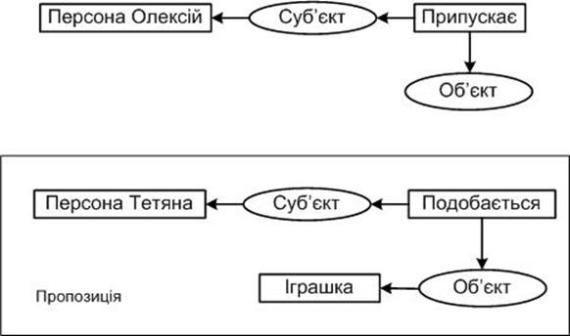
   Рисунок 3.14 Концептуальний граф, що містить пропозицію
   

   Введення окремих блоків для позначення пропозицій дозволяє фіксувати відносини між пропозиціями. У приведеному прикладі дієслово “думає” представляє не конкретна фізична дія, а виражає відчуття Олексія. Тому на графі введене нове відношення “суб’єкт”, що представляє обличчя, що випробує ті чи інші відчуття. Твердження, що містять подібні лексичні одиниці (довіряти, вірити, мати намір і т.п.) є об’єктом досліджень модальної логіки.
   

   Концептуальний граф дозволяє природним образом виражати кон’юнкцію. Наприклад, за допомогою концептуального графа ми легко можемо представити пропозицію “Собака знаходилася в саду і гризла кісту”. Складніше з іншими логічними операціями: диз’юнкцією, логічним запереченням, кванторами.
   

   Для представлення заперечення на концептуальних графах, застосовується унарный логічний оператор “не”. Оператор застосовують до пропозиції. Твердження, що фіксується пропозицією, вважається в цьому випадку помилковим. Граф, зображений на рисунку 3.15, відповідає пропозиції: “Немає іграшок, що подобаються Тетяні”.
   

   Використовуючи заперечення і кон’юнкцію, можна представити на концептуальних графах диз’юнкцію. Однак для спрощення концептуальних схем диз’юнкцію представляють у вигляді спеціального бінарного відношення “чи”, аргументами якого є вершини-пропозиції.
   

   
   

   Рисунок 3.15 – Концептуальний граф з логічним запереченням
   

   Узагальнені поняття-об’єкти-поняття, відображувані на концептуальних графах, зв’язані квантором існування. Так, граф, зображений на рисунку 3.10, можна описати формулою
   

   (м’яч (х) колір (x, y) червоний (y)).
   

   Квантор спільності виходить при запереченні пропозицій, зв’язаних квантором існування. Наприклад, застосувавши заперечення до графа, зображеному на рисунку 3.10, одержимо
   

   (м’яч (х) колір (х, у) 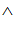червоний (у)).
   

   По своїх виразних можливостях концептуальні графи еквівалентні логіці числення предикатів. Існує можливість взаємного переходу від описів предметної області мовою числення предикатів до концептуальних графів, і навпаки. Вибір тих чи інших засобів визначається характером розв’язуваних задач і схильностями розроблювачів СШІ.
   

   Методи виводу на семантичних мережах використовують асоціативні й алгоритми, що зіставляють, що зводяться до перебування шляхів на графі, побудові транзитивних замикань, вигляділенню підграфів з визначеними властивостями. Основні підходи до побудови процедур виводу на семантичних мережах викладені в [8,29,34]. У багатьох випадках вони базуються на простих операціях над графами,: видалення і додавання нових вершин і ребер, спеціалізація, пошук вершини чи ребра по імені, перехід від однієї вершини до іншої по зв’язках, об’єднання підграфів і ін.
   

   Одним із простих засобів виводу на семантичних мережах є пошук по перетинанню, що був розглянутий раніше.
   

   Іншим могутнім засобом виводу є зпівставлення зі зразком. У даному випадку відбувається зпівставлення окремих фрагментів семантичної мережі. При цьому запит до бази знань представляється у вигляді автономного підграфа, що будується за тими ж правилам, що і семантична мережа. Пошук відповіді на запит реалізується зпівставленням підграфа запиту з фрагментами семантичної мережі. Для цього здійснюють накладення підграфа запиту на відповідний фрагмент мережі. Успішним буде те накладення, у результаті якого фрагмент мережі виявляється ідентичним підграфу запиту. При цьому допускається використання в запиті змінних. Змінна запиту зіставляється з константою фрагмента мережі. Нехай, наприклад, є запит: ” чи існує такий птах X, що вміє пекти і має жовтий колір?” (Рисунок 3.16).
   

   
   

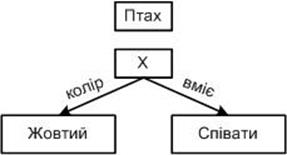
   Рисунок 3.16 – Підграфа запиту
   

   Ізоморфне вкладення підграфа запиту в семантичну мережу, зображену на рисунку 3.7, дозволяє дати відповідь Х=”канарка”.
   

   У загальному випадку в підграфі запиту можуть бути задані об’єкти, атрибути, імена відносин, не представлені в базі знань явно. Це вимагає виконання попередніх перетворень фрагментів семантичних мереж, що зіставляються. У результаті таких перетворень можуть бути отримані нові зв’язки. Зазначені перетворення виконуються на основі найпростіших базових операцій розглянутих раніше.
   

   Методи виводу на семантичних мережах, що використовують ідею перетинання чи шляхів зпівставлення фрагментів мереж, мають істотний недолік. Він зв’язаний з комбінаторним ростом числа чи зіставлень перетинань у мережах досить великої розмірності.
   

   У ряді систем, заснованих на семантичних мережах, використовуються спеціалізовані правила виводу. У [8] розглядаються методи дедуктивного виводу на семантичних мережах, засновані на поняттях розфарбування графів і операторах перетворення мереж.